ALGORITMO DIJKSTRA

 ALGORITMO DIJKSTRA

Descripción

El algoritmo de dijkstra determina la ruta más corta desde un nodo origen hacia los demás nodos para ello es requerido como entrada un grafo cuyas aristas posean pesos. Algunas consideraciones:

• Si los pesos de mis aristas son de valor 1, entonces bastará con usar el algoritmo de BFS.
• Si los pesos de mis aristas son negativos no puedo usar el algoritmo de dijsktra, para pesos negativos tenemos otro algoritmo llamado Algoritmo de Bellmand-Ford.

Conjunto C : Conjunto de vértices candidatos. Inicialmente contiene todos los nodos menos el nodo origen. 
Conjunto S : Conjunto de vértices seleccionados, es decir, aquellos para los que ya conocemos su camino mínimo desde el nodo origen. Inicialmente contiene el nodo origen. 
Vector D : Almacenará la longitud del camino más corto desde el origen a cada nodo. Tendrá tantas posiciones como nodos tenga el grafo. El coste de ir del nodo origen a sí mismo lo estimaremos como cero. 
Vector P : Almacenará el nodo predecesor a cada nodo en el camino más corto desde el origen hasta él. Tendrá tantas posiciones como nodos tenga el grafo. La posición del nodo predecesor al origen estableceremos que sea cero para indicar que es el nodo origen.
Llamaremos al nodo origen o, y el coste de ir del nodo i al nodo j lo denotaremos como COSTEij .

Los pasos a seguir para el algoritmo de dijkstra:

 Seleccionamos el nodo que sea destino de la arista con menor valor que salga del nodo o, llamémoslo u. Introducimos el nodo u en S y lo sacamos de C. Almacenamos en la posición u del vector D el valor COSTEou y en la posición u del vector P el valor del nodo predecesor, es decir, o.

Seleccionamos el siguiente nodo al que podamos llegar con menor coste, bien directamente desde o, bien a través del otro nodo seleccionado u. Llamamos al nuevo nodo seleccionado v. Introducimos el nodo v en S y lo sacamos de C. Introducimos en la posición v del vector D el coste de llegar al nodo v, si es directamente desde o será COSTEov, si es a través de u será D[u]+COSTEuv. Por último, en la posición v del vector P introducimos el valor del nodo predecesor, ya sea o o u.

Repetiremos este proceso hasta que todos los nodos hayan sido seleccionados, es decir, hasta que el conjunto C esté vacío, o lo que es lo mismo, hasta que en el conjunto S se encuentren todos los nodos del grafo. En ese momento en el vector D tendremos almacenado el coste mínimo para llegar desde el nodo origen a cualquier nodo del grafo, y podremos obtener el camino más corto mediante el vector P.

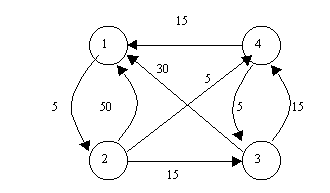
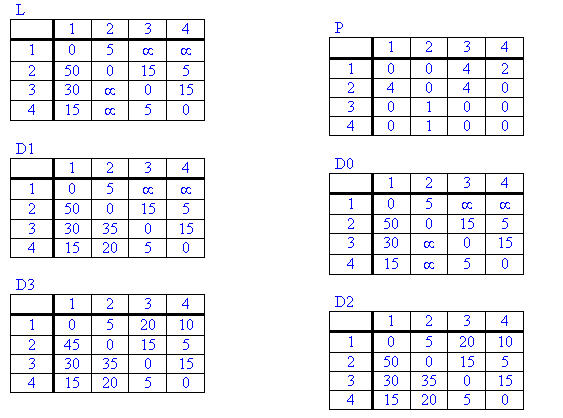
 EJEMPLO1:

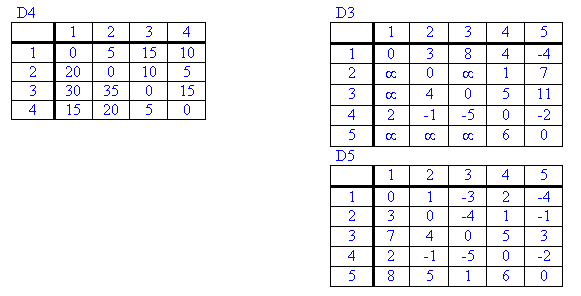
 EJEMPLO2:

 

 

GRAFOS Y CAMINO MAS CORTO

 DISKTRA

FLOYD 

cuestinario

ALGORITMO FLOYD

ALGORITMO FLOYD

El algoritmo de Floyd es más general que el de Dijkstra, ya que determina la ruta más corta entre dos nodos cualquiera de la red.

• El algoritmo representa una red de n nodos como una matriz cuadrada de orden n, la llamaremos matriz C. De esta forma, el valor Cij representa el coste de ir desde el nodo i al nodo j, inicialmente en caso de no existir un arco entre ambos, el valor Cij será infinito.
• Definiremos otra matriz D, también cuadrada de orden n, cuyos elementos van a ser los nodos predecesores en el camino hacia el nodo origen, es decir, el valor Dij representará el nodo predecesor a j en el camino mínimo desde i hasta j. Inicialmente se comienza con caminos de longitud 1, por lo que Dij = i.
• Las diagonales de ambas matrices representan el coste y el nodo predecesor para ir de un nodo a si mismo, por lo que no sirven para nada, estarán bloqueadas.

los pasos a seguir del algoritmo de Floyd son: 

• Formar las matrices iniciales C y D.
• Se toma k=1.
• Se selecciona la fila y la columna k de la matriz C y entonces, para i y j, con i≠k, j≠k e i≠j, hacemos:

Si (Cik + Ckj) < Cij → Dij = Dkj y Cij = Cik + Ckj

En caso contrario, dejamos las matrices como están. 

• Si k ≤ n, aumentamos k en una unidad y repetimos el paso anterior, en caso contrario paramos las iteraciones.
• La matriz final C contiene los costes óptimos para ir de un vértice a otro, mientras que la matriz D contiene los penúltimos vértices de los caminos óptimos que unen dos vértices, lo cual permite reconstruir cualquier camino óptimo para ir de un vértice a otro.

EJEMPLO:

TIPOS DE GRAFOS

DEFINIMOS: Se dice que el grafo G = (V, E) es:


a)      un grafo regular de grado n si todos sus vértices tienen grado n.

 

Grafos regulares de grado 2.

 

Grafos regulares de grado 3.

b)      un grafo completo si cada par de vértices está unido por una arista. Se denota por K_n al grafo completo de n vértices

 

c)      un ciclo si V = {v₁, v₂, . . . v_n},  n³> 3, y  E = {(v₁, v₂), (v₂, v₃), . . . , (v_n, v₁)}. Se denota por C_n al ciclo de n vértices

 

d)      una rueda si V = {v₀, v1, v₂, . . . v_n}, n n> 3, y E = {(v₁, v₂), (v₂, v₃), . . . , (v_n, v₁), {(v₁, v₀), (v₂, v₀), . . . , (v_n, v₀) }. Se denota por W_n a la rueda de n+1 vértices

 

e)      un cubo si sus vértices y aristas están relacionados como los de un cubo n-dimensional. Se denota por Q_n al cubo asociado al cubo n-dimensional.

 

f)        un grafo bipartido si V=V₁UV₂ y cada arista de E une un vértice de V₁ y otro de V₂

 

_{g)      un grafo bipartido completo si V=V1UV2 y dos vértices de V están unidos por una arista de E si y solo si un vértice está en V1 y el otro en V2. Se denota por Kr,s al grafo bipartido completo donde V1 tiene r vértices y V2 tiene s vértices}

        

CONCEPTOS BASICOS

 GRAFOS

Esta propiedad hace a los grafos las estructuras más adecuadas para representar situaciones donde la relación entre los elements es completamente arbitraria, como pueden ser mapas de carreteras, sistemas de teleco municaciones, circuitos impresos o redes de ordenadores. Aunque hay estructuras más complejas que los graf os, no las veremos en este curso. Los grafos se pueden clasificar en diferentes tipos dependiendo de cómo se defina la relación entre los elementos: podemos encontrar grafos dirigidos o no di rigidos y etiquetados o no etiquetados. También se pueden combinar ambas categorías.

 LOS PROBLEMAS A CONOCER DE CAMINOS MAS CORTOS

Los problemas del camino mínimo o camino más corto, tratan como su nombre indica de hallar la ruta mínima o más corta entre dos puntos. Este mínimo puede ser la distancia entre los puntos origen y destino o bien el tiempo transcurrido para trasladarse desde un punto a otro. Se aplica mucho para problemas de redes de comunicaciones.

Aristas

Son las líneas con las que se unen las aristas de un grafo y con la que se construyen también caminos.
Si la arista carece de dirección se denota indistintamente {a, b} o {b, a}, siendo a y b los vértices que une.
Si {a ,b} es una arista, a los vértices a y b se les llama sus extremos.

• Aristas Adyacentes: Se dice que dos aristas son adyacentes si convergen en el mismo vértice.
• 
  
• Aristas Paralelas: Se dice que dos aristas son paralelas si vértice inicial y el final son el mismo.
• 
  
• Aristas Cíclicas: Arista que parte de un vértice para entrar en el mismo.
• 
  
• Cruce: Son dos aristas que cruzan en un punto.
• 
  

Vértices

Son los puntos o nodos con los que esta conformado un grafo. Llamaremos grado de un vértice al número de aristas de las que es extremo. Se dice que un vértice es `par' o `impar' según lo sea su grado.

• Vértices Adyacentes: si tenemos un par de vértices de un grafo (U, V) y si tenemos un arista que los une, entonces U y V son vértices adyacentes y se dice que U es el vértice inicial y V el vértice adyacente.
• Vértice Aislado: Es un vértice de grado cero.
• 
  
• Vértice Terminal: Es un vértice de grado 1.
• 
  

Caminos

Sean x, y " V, se dice que hay un camino en G de x a y si existe una sucesión finita no vacía de aristas {x,v1}, {v1,v2},..., {vn,y}. En este caso

• x e y se llaman los extremos del camino
• 
  
• El número de aristas del camino se llama la longitud del camino.
• 
  
• Si los vértices no se repiten el camino se dice propio o simple.
• 
  
• Si hay un camino no simple entre 2 vértices, también habrá un camino simple entre ellos.
• 
  
• Cuando los dos extremos de un camino son iguales, el camino se llama circuito o camino cerrado.
• 
  
• Llamaremos ciclo a un circuito simple
• 
  
• Un vértice a se dice accesible desde el vértice b si existe un camino entre ellos. Todo vértice es accesible respecto a si mismo