ALGORITMO FLOYD

ALGORITMO FLOYD

El algoritmo de Floyd es más general que el de Dijkstra, ya que determina la ruta más corta entre dos nodos cualquiera de la red.

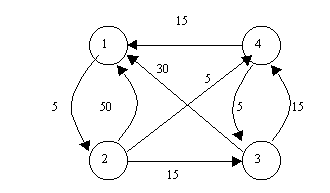
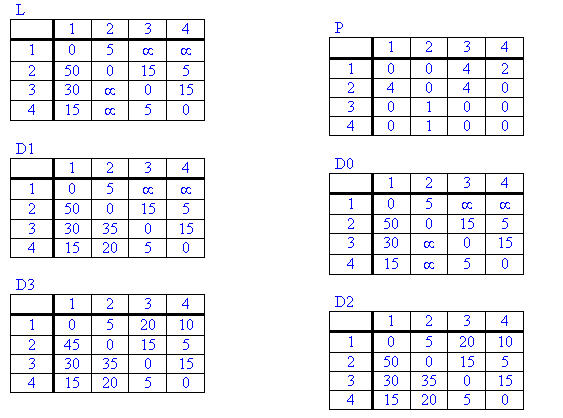
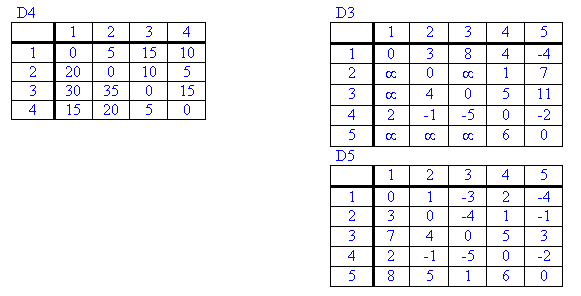
• El algoritmo representa una red de n nodos como una matriz cuadrada de orden n, la llamaremos matriz C. De esta forma, el valor Cij representa el coste de ir desde el nodo i al nodo j, inicialmente en caso de no existir un arco entre ambos, el valor Cij será infinito.
• Definiremos otra matriz D, también cuadrada de orden n, cuyos elementos van a ser los nodos predecesores en el camino hacia el nodo origen, es decir, el valor Dij representará el nodo predecesor a j en el camino mínimo desde i hasta j. Inicialmente se comienza con caminos de longitud 1, por lo que Dij = i.
• Las diagonales de ambas matrices representan el coste y el nodo predecesor para ir de un nodo a si mismo, por lo que no sirven para nada, estarán bloqueadas.

los pasos a seguir del algoritmo de Floyd son: 

• Formar las matrices iniciales C y D.
• Se toma k=1.
• Se selecciona la fila y la columna k de la matriz C y entonces, para i y j, con i≠k, j≠k e i≠j, hacemos:

Si (Cik + Ckj) < Cij → Dij = Dkj y Cij = Cik + Ckj

En caso contrario, dejamos las matrices como están. 

• Si k ≤ n, aumentamos k en una unidad y repetimos el paso anterior, en caso contrario paramos las iteraciones.
• La matriz final C contiene los costes óptimos para ir de un vértice a otro, mientras que la matriz D contiene los penúltimos vértices de los caminos óptimos que unen dos vértices, lo cual permite reconstruir cualquier camino óptimo para ir de un vértice a otro.

EJEMPLO: